与轴对称有关的最小值问题
与轴对称有关的最小值问题
如图,在直线l同侧有两点A、B,在直线l上求作一点P使PA+PB的值最小。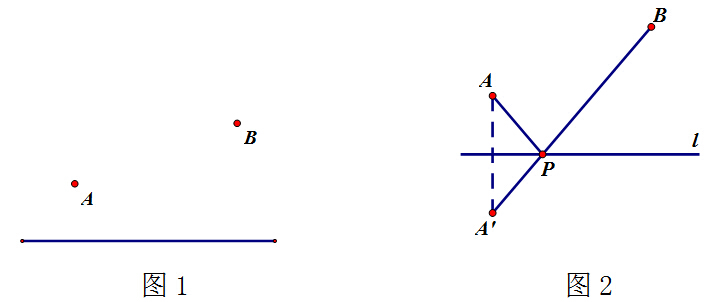
解题思路:涉及最短距离的问题,一般依靠的知识点是 “两点之间线段最短”,我们可以通过轴对称的知识帮助找到可以连接线段的两个点,多数情况下,首先要作点关于某直线的对称点.
解:如图2,作点A关于l的对称点A′,连接A′B,交l于点P,点P即为所求.
∵点A和点A′关于直线l对称,且点P在l上,
∴PA=PA′,
又∴A′B交l于点P,且两条直线相交只有一个交点,
∴PA′+PB最短,
即PA+PB的值最小.
练习:
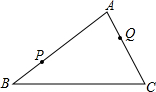
(1)P、Q分别是△ABC的边AB,AC上的点,在BC上求做一点R,使△PQR的周长为最短,写出作法.
答案:
(1)P、Q分别是△ABC的边AB,AC上的点,在BC上求做一点R,使△PQR的周长为最短,写出作法.

解题方法:题中PQ长度固定,找△PQR的最小值,即为找PR+QR的最小值,作法如下:
1.做点P关于BC的对称点P’ ;
2.连接P’Q交BC于R;
3.连接PR。

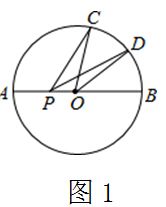
(2)如图1,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°,弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为 。

解题思路:(如图2)
1.根据轴对称,作出点C关于AB的对称点C′,连接DC′交AB于点P,此时PC+PD最小.
2.由题意求出弧DB的度数为40°,进而得到弧DBC′的度数为120°,算出∠DOC′的度数为120°,从而得到∠DOE的度数为60°
3.在Rt△DEO中,利用三角函数或勾股定理计算出DE的长为 ,再根据垂径定理可以得到DC′的长为 R, R即为PC+PD的最小值.