平面直角坐系中的“找规律”题型
平面直角坐系中的“找规律”题型
平面直角坐标系中的这类题目看上去比较复杂,实际上,关键性的内容并不多。解决本类题目的主要方法:
1.对题目做一番认真地分析,去粗取精,取伪存真,把其中主要的、关键的内容抽出来,题目的难度就会大幅度降低。
2.所谓找规律,多数情况下,是指变量的变化规律,所以最重要的是找出变量的变化规律。
3.把变量和序号放在一起加以比较,将规律表示出来。或将题目中的问题解答出来。
练习题:
1.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是( )1.对题目做一番认真地分析,去粗取精,取伪存真,把其中主要的、关键的内容抽出来,题目的难度就会大幅度降低。
2.所谓找规律,多数情况下,是指变量的变化规律,所以最重要的是找出变量的变化规律。
3.把变量和序号放在一起加以比较,将规律表示出来。或将题目中的问题解答出来。
练习题:
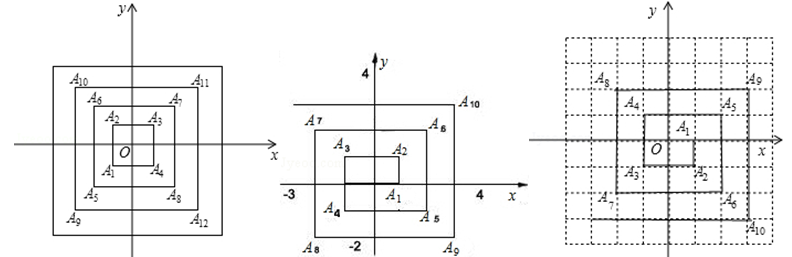
第1题图 第2题图 第3题图
A.(13,13)B.(﹣13,﹣13)C.(14,14)D.(﹣14,﹣14)
2.如图,已知Al(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),….则点A2007的坐标为 _________ .
3.如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2010的坐标是 _________ .
4.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.


(1)填写下列各点的坐标:A4( , ),A8( , ),A12( , );
(3)指出蚂蚁从点A100到点A101的移动方向.
参考答案:
1.C
答案解析:∵2007=4×501+3,∴A2007与A3在同一象限,即都在第一象限,
根据题中图形中的规律可得:
3=4×0+3,A3的坐标为(0+1,0+1),即A3(1,1),
7=4×1+3,A7的坐标为(1+1,1+1),A7(2,2),
11=4×2+3,A11的坐标为(2+1,2+1),A11(3,3);
∴55=4×13+3,A55(14,14),A55的坐标为(13+1,13+1);
2. (-502,502)
答案解析:∵55=4×13+3,∴A55与A3在同一象限,即都在第二象限,
根据题中图形中的规律可得:
3=4×0+3,A3的坐标为(-0-1,0+1),即A3(-1,1),
7=4×1+3,A7的坐标为(-1-1,1+1),A7(-2,2),
11=4×2+3,A11的坐标为(-2-1,2+1),A11(-3,3);
∴2007=4×501+3,A2007(-502,502),A2007的坐标为(-502,502);
3. (502,-502)
答案解析: ∵2010=4×502+2,∴A2010与A2在同一象限,即都在第四象限,
根据题中图形中的规律可得:
2=4×0+2,A2的坐标为(0+1,0-1),即A3(1,-1),
6=4×1+2,A6的坐标为(1+1,-1-1),A7(2,-2),
10=4×2+2,A10的坐标为(2+1,-2-1),A11(3,-3);
∴2010=4×502+2,A2010(502,-502),A55的坐标为(502,-502);
4.答案解析:
(1)由图可知,A4,A12,A8都在x轴上,
∵小蚂蚁每次移动1个单位,
∴OA=2,OA8=4,OA12=6,
∴A4(2,0),A8(4,0),A12(6,0);
同理可得出:A10(5,1),;
故答案为:2,0;4,0;5,1;6,0;
(2)根据(1)OA4n=4n÷2=2n,
∴点A4n的坐标(2n,0);
(3)∵100÷4=25,
∴从点A100到点A101的移动方向与从点A4到A5的方向一致,为向上.