探究特殊四边形的存在问题题型
哈尔滨中考数学研究专题,本期整理分享探究特殊四边形的存在问题题型,供广大老师、学生、课外辅导参考之用。
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
1.如图,已知直线y=-43
x+8与x轴交于点A,与y轴交于点B,C是线段AB的中点,抛物线y=ax2+bx+c(a>0)过O、
A两点,且其顶点的纵坐标为-43
(1)分别写出A、B、C三点的坐标;
(2)求抛物线的函数解析式;
(3)在抛物线上是否存在点P,使得以O、P、B、C为顶点的四边形是菱形?若存在,求所有满足条件的点P的坐标;若不
存在,请说明理由.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A、B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛
物线的解析式;若不存在,请说明理由.
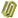 |
特殊四边形的存在问题 |